Machine Scheduling, Machine Learning in Engineering

投稿日 編集日 カテゴリ

Perface

叨叨几分钟。

写这篇文章，其实仅标题就琢磨了许久，无法找到确切和顺畅的词语来描述这个事情，撇开信达雅，似乎能勉强表述为：一种结合机器学习和数学模型的方法进行平台流程开发优化的例子。然后最终还是选择了现在这个标题，不过有点意思，其中两个Machine的意义其实是不同的，后续我们会再展开。

说来这个case其实已经存在许久，5年前还在O记的时候，在一次数据开发并行化的任务中发现的方法。起初刚开始采用的方法比较稚嫩，有点惭愧就在此不表，直到后续闲暇下来之后再重新考虑这个问题时候，想到了还在学校惨遭延毕的博士同窗，徐徐聊起来，才发现原来是一个可以结合离散优化和机器学习的典型应用。离开O记之后，或多或少有时还是会联想到这个问题，但总会得到一些新的感悟，也有幸有时间进行了更深度的研究和探索。不过最近再看这个问题时，发现当初解决的思路和逻辑有些竟已忘却，就觉得很有必要把这些记录下来，除了对自己，也对这个问题能有个比较好的交代吧。

Parallelism

上面提到的数据开发并行化其实是一个单机程序进行多机并行化的任务，依稀还记得当初接手这个程序的无语，也是第一次接触如此复杂的Python程序，正是由于这个经历，后面看到“怕他”这样程序并没有受到更多的震撼。这段程序的原始作者是自己的老板和另外一个高高瘦瘦的犹太人，还记得他的名字Ian langmore，男神，初次见的分离式键盘就是他安利的。他是自己在O记这段时间中为数不多合作比较深入的geeker，记得最后他离开O记的时候，farewell中给每个人留了一句话，也是一个温暖且又细腻的人。

这个程序本身是一个集合了multinomial logistic regression以及markov chain的scoring program（也可能是monte carlo simulation，对stochastic process并不熟，忘了是哪个mc，请原谅这个数学系学渣的笔者😑）。程序中计算部分逻辑复杂晦涩，又是probabality又是matrix，而如果对其进行逻辑的拆分硬套MR框架，实现难度不小，且本身程序的效率问题更多是处理量和处理单元数量悬殊的问题，所以解决这个问题的思路还是想通过分而治之的方式进行分流，直观上难度似乎很低：工程师只需要利用map和shuffle的特性进行任务分发即可完成。

但这个过程中仔细想想会发现有个很有意思的问题，当然这也是取决于这个任务的特性。

  1. 首先，这个任务需要处理的数据可以看作为是n多的“Group“，而每个“Group”又包含了很多明细数据，明细数据量的分布并不是一个均匀分布，方差实际会比较大。

  2. 其次，程序处理一个Group的耗时即效率和Group本身包含的数据量成一定的正比关系。

基于这样的条件，我们是否还会采用MR默认的Partition进行分流？这样是不是会引起典型的data skew问题，有没有更好的Partition方法来提高整体的效率？

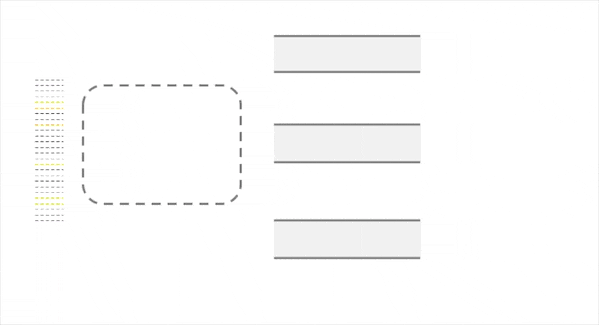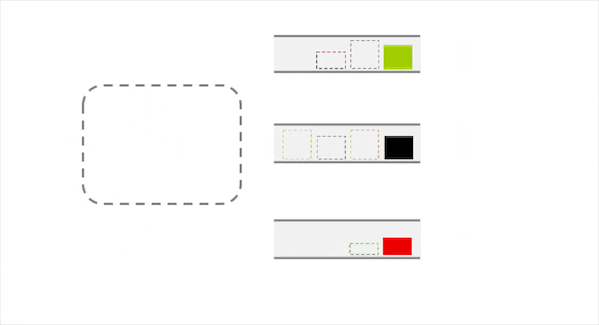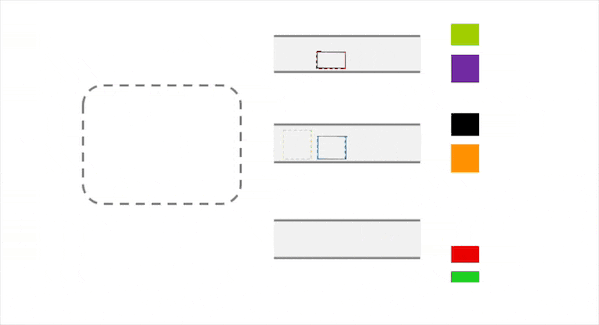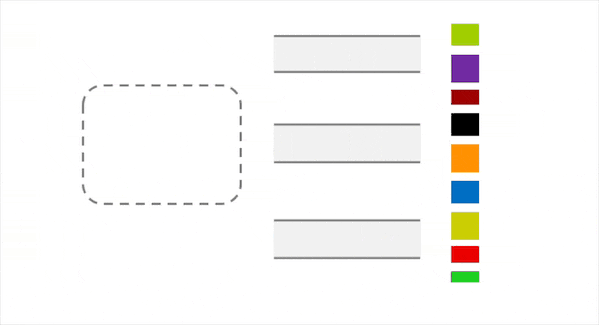
事实上，如上图所示，默认的Partition可能会导致data skew的问题，缘由其做分配时采用的key与key的属性无关，仅与key本身的值相关。因此，我们希望能有一种调度算法使得分配结果更合理，如下图所示。

Job Shop

Job-shop，中文叫车间调度，是一个离散的最优化问题，又称为Multiprocessor Scheduling，是一个非常典型的基于Machine Scheduling的运筹问题。可以看一下表述：”Given a set J of jobs where job has length and a number of processors m, what is the minimum possible time required to schedule all jobs in J on m processors such that none overlap?” 换言之，即有一堆大小不同的任务需要由若干个相同产能的机器进行处理，那么整个过程耗时最短时间会是多少？也有另外一种问法，如何安排可以使得最后处理完成的的机器耗时最小？

这个问题的本质其实和上面提到的问题基本相同，map processor可以看作若干个产能相同的机器，而Group可以看作大小不一的job，所以类比Job-shop，核心问题Partition的设计即Job-shop中的scheduling。

不过很遗憾，Job-shop本身是一个NP-hard的问题，即要得到最优解非遍历解空间几乎不可能，因此我们需要找到近似方法来解决这个问题，而事实上车间调度并不是一个新的问题，问题很简单，在学术界存在了许久，有很多相关paper和方法来来近似最优解，例如遗传算法。但由于我们需要的是一个Partition，shuffle的特点即快，所以如果使用了非常复杂的方法置于Partition的过程，其实是非常不合适的。

LPT

LPT也有称为LPTF，Largest(Longest, Least) Processing Time First。是一种解决车间调度问题的近似方法，顾名思义，最大的任务先做。

这个方法过程非常∞简单，很适合用来作Parition：每个机器machine维护自己要处理的任务job队列，然后从任务中选择最大的任务，分配给当前任务队列中任务耗时总和最小的机器，如果最小的机器超过一个，则随机分配给其中一个。这个过程实施过程中，分配和处理是分离的。因此逻辑上可以直接应用到Partition的设计上。

当初在做这个task时候，由于项目紧张的缘故，我也仅仅了解了这个方法的上界是最优解的4/3。直到后续深入这个方法的证明时觉得挺有意思，可以再理解下。那么接下来介绍下其证明原理。

Definition 1

我们假设给定 个machine， 个job，其中job 需要耗时 。 表示为machine i的load。

Lemma 1

  • 引理：设 是最后一个需要完成的任务，则 。
  • 证明：由于是最后一个完成的任务，则最后一个任务分配之前，m个machine中存在load最小的load，令其为。因此，显而易见，最小的load的m倍一定小于等于其他所有任务load的总和，表示为 ，等价于， 。因此，我们可以得到：

    证毕。

Lemma 2

  • 引理：适用于任意情况，如果限制最优解在每台machine上最多分配两个任务，则LPT调度算法得到的结果即最优解。

  • 证明：不失一般性，我们假设job的数量n和机器的数量m呈以下关系：。由于引理中的限制前提，其实无法处理更多的job数量，此外如果job数量小于2m，则我们可以补充一些耗时为0的dummy jobs。相似地，我们使用这样的表述 来表示耗时关系 。我们同时也假设所有job的耗时皆不同，且当如果最小load的machine有多台，LPT会选择其中机器标识最小的机器作分配，而不是随机。

    此外，我们使用 和 表示机器i中被分配的最大job和最小job的标识。现在我们可以模拟最优解的过程，看是否能逼近LPT算法的结果。

    1. 假设存在任意两个机器i和j，满足 ，我们需要先交换job 和 。对所有满足条件的任意两个机器重复此过程后，我们可以得到，top m大的任务会分配给每台机器上。
    2. 其次，对任意两个机器i和j，满足 和 ，我们交换job 和 ，以及 和 。在所有满足条件的机器重复此过程后，我们可以得到 的order为 。
    3. 最后，对任意两个机器i和j，满足 和 ，我们交换job 和 。由于 ，这步并不会增加最大的load。我们最终会得到 的order为 ， 的order为 。

    这个优化方法得到最终每个job的order与LPT得到的结果一致。证毕。

Definition 2

一个算法如果对所有情况皆可满足近似率 ，其算法可以得到一个解 满足 ，其中 表示为最优解。

LPT的近似率即上界即为4/3，接下来进行证明。

Theorem

  • 定理：对于车间调度问题，LPT的近似率为 ，m为Definition 1中定义的机器数量。

  • 证明：反证，假设定理是错误的，即成立：

    然后利用Lemma 1，我们可以得到，设 是最后一个需要完成的任务：

    由于最优解显然大于等于所有耗时的平均值： 。

    进行约化，可得：

    由于 是最小的job，这个公式说明了对于最优解 ，没有任何机器可以被分配两个以上的job。因此套用Lemma 2的结论，LPT算法得到结果即是最优解：

    考虑 中m取值1时，等式右边达到最小值，可以得到：

    因此 和 矛盾，假设不成立，定理得证。

Implement

LPT代码的实现非常简单，核心代码3、4行即可。其余的部分，交给MR框架进行实现。

1
2
3
4
5
6
import random
jobs = random.sample(xrange(100), 10) # init jobs
jobs = sorted(jobs, reverse=True) # sort jobs
machines = [[] for i in xrange(3)] # init machines
map(lambda x:min(machines, key=sum).append(x), jobs) # LPT scheduling
print machines

Machine Learning

至此还没有提到和机器学习相关的任何东西，不过在这个case，机器学习的应用相对简单很多。前文提到Group中的明细数据量和Group的耗时成正比，因此我们可以利用Group中的明细数据对Group被计算的耗时进行预估，这是一个比较典型的Linear Regression，甚至可以是univariate的。当我们模型完成后，只要在LPT进行分配的时候，对数据量进行模型打分得到最终的耗时，再进行分配即可，由于模型参数是一个可忽略不计大小的配置，其对效率也基本不会有任何影响。

再进一步，我们甚至可以利用online-learning的方法不断去optimize这个univariate的regression，所以最终会是一个结合MS和ML的工程优化实例。

Summay

  • Operation Research & Cybernetic是在Machine Learning以及Data Mining之前，数学领域在工业界主要的应用方向。与ML的连续性问题不同，大多case是离散问题，特点不一定需要很多数据，依靠算法和技巧解决一些实际的工业流程优化问题。所以一般的工具，matlab就够。不过对理论基础要求很高，和高校举办的数学模型内容比较相似。而且近两年，随着交通、物流、外卖类服务的互联网智能化越来越深入，各大厂也开始大肆招募OR方向优化的能人，从长远的发展来看，其应用具备非常独立的场景，前景看好。
  • 随着ML的大热，OR领域也迎来不少新的突破，有些新的方法加入了ML的元素。然而另一方面，趋势引领潮流，一般的研发工作可能无法直接和分析、模型接触，甚至连算法也被越来越多的开源项目给封装，套路变多了，新鲜的挑战似乎变少了。但谁又不曾折腾过呢，ML、DM的数学思维方式背后，又或许会打开通外另外世界的窗口。实话说，可以去尝试，可以去思考，应用一些新潮流的元素，创造一些新的解决方案，也不失为一种创新的契机。
  • 最后共勉一句话吧：Unless you try to do something beyond what you have alredy mastered, you will never grow.